A constant force F = m₂g/2 is applied on the block of mass m₁ as shown in fig. The string and the pulley are light and the surface of the table is smooth. The acceleration of m₁ is

\(\frac{m_{2}g}{2(m_{1}+m_{2})}\) towards right
\(\frac{m_{2}g}{2(m_{1}-m_{2})}\) towards left
\(\frac{m_{2}g}{2(m_{2}-m_{1})}\) towards right
\(\frac{m_{2}g}{2(m_{2}-m_{1})}\) towards left

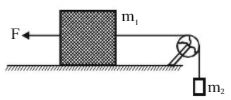
Solution

Fig. shows a uniform rod of length 30 cm having a mass of 3.0 kg. The strings shown in the figure are pulled by constant forces of 20 N and 32 N. All the surfaces are smooth and the strings and pulleys are light. The force exerted by 20 cm part of the rod on the 10 cm part is

20 N
24 N
32 N
52 N

Solution

A force time graph for the motion of a body is shown in Fig.Change in linear momentum between 0 and 8s is

zero
4N-s
8Ns
None of these

Solution

Change in momentum= Force × time = Area which the force-time curve encloses with time axis.

A machine gun has a mass 5 kg. It fires 50 gram bullets at the rate of 30 bullets per minute at a speed of 400 ms^-1. What force is required to keep the gun in position?

10 N
5 N
15 N
30 N

Solution

A uniform rope of length L resting on a friction less horizontal surface is pulled at one end by a force F. What is the tension in the rope at a distance ι from the end where the force is applied.

F
F (1 + ι/L)
F/2
F (1 – ι/L)

Solution

Let n be the mass per unit length of rope. Therefore,mass of rope = nL.

Acceleration in the rope due to force F will be a = F/nL.

Mass of rope of length (L– ι) will be n (L – ι).

Therefore, tension in the rope of length (L – ι), is equal to pulling force on it

= n (L – ι) a =n (L – ι) × F/nL =F (1 – ι/L)

A car travelling at a speed of 30 km/h is brought to a halt in 4 m by applying brakes. If the same car is travelling at 60 km/h,it can be brought to halt with the same braking power in

8 m
16 m
24 m
32 m

Solution

As, (1/2)m v²= Fs

So ¹⁄₂m(30)²=F × 4 and ¹⁄₂ m(60)²=F × s

∴ s/4 = (60)²/(30)²= 4 or s =4 × 4 = 16 m

A player stops a football weighting 0.5 kg which comes flying towards him with a velocity of 10m/s. If the impact lasts for 1/50th sec. and the ball bounces back with avelocity of 15 m/s, then the average force involved is

250 N
1250 N
500 N
625 N

Solution

Here m = 0.5 kg ; u = –10 m/s ;

t = 1/50 s ; v =+ 15 ms^–1

Force = m(v– u)/t = 0.5 (10 + 15) × 50 = 625 N

A toy gun consists of a spring and a rubber dart of mass 16g. When compressed by 4cm and released, it projects the dart to a height of 2 m. If compressed by 6 cm, the height achieved is

3 m
4 m
4.5 m
6 m

Solution

If k is the spring factor,then P.E. of the spring compressed by distance x (=¹⁄₂ Kx²) will equal to gain in P.E. of the dart ( = mgh) i.e. ¹⁄₂ kx² = mgh

∴ ¹⁄₂ k (4)²= 16 × g × 200 ....(i)

and ¹⁄₂ k (6)²= 16 × g × h ...(ii)

On solving, (i) and (ii), we get h = 450 cm = 4.5 m.

A solid sphere of 2 kg is suspended from a horizontal beam by two supporting wires as shown in fig. Tension in each wire is approximately (g = 10 ms^–2)

30 N
20 N
10 N
5 N

Solution

2 T cos 60º = mg or T = mg = 2×10 = 20N.

An object of mass 10 kg moves at a constant speed of 10 ms^–1. A constant force, that acts for 4 sec on the object,gives it a speed of 2 ms–1 in opposite direction. The force acting on the object is

–3 N
–30 N
3 N
30 N

Solution

UnAttempted

0

Attempted

0

Correct

0

Wrong

0

Complete