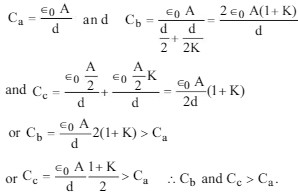The capacitance of a parallel plate capacitor is C_a(Fig. a). A dielectric of dielectric constant K is inserted as shown infig (b) and (c). If C_b and C_c denote the capacitances in fig(b) and (c), then

both C_b, C_c > C_a
C_c > C_a while C_b > C_a
both C_b, C_c < C_a
C_a= C_b = C_c

Solution

Two spherical conductors A and B of radii a and b (b > a)are placed concentrically in air. B is given charge +Q and A is earthed. The equivalent capacitance of the system is

4πε₀\(\frac{ab}{b-a}\)
4πε₀(a + b)
4πε₀b
4πε₀\(\frac{b^{2}}{b-a}\)

Solution

If we increase ‘d’ of a parallel plate condenser to ‘2d’ and fill wax to the whole empty space between its two plate, then capacitance increase from 1pF to 2pF. What is the dielectric constant of wax?

Solution

Three capacitors each of capacity 4μF are to be connected in such a way that the effective capacitance is 6 μF.This can be done by

connecting two in parallel and one in series
connecting all of them in series
connecting them in parallel
connecting two in series and one in parallel

Solution

If a slab of insulating material 4 × 10^-5m thick is introduced between the plates of a parallel plate capacitor,the distance between the plates has to be increased by 3.5 × 10^-5m to restore the capacity to original value. Then the dielectric constant of the material of slab is

Solution

As x = t(1 - ¹⁄_K), where x is the addition distance of plate,to restore the capacity of original value.

∴ 3.5 × 10^-5 = 4 × 10^-5 (1 - ¹⁄_k)

Solving, we get,K =8.

A circuit is connected as shown in the figure with the switch S open. When the switch is closed, the total amount of charge that flows from Y to X is

zero
54 μC
27 μC
81 μC

Solution

When steady state is reached, the current I coming from the battery is given by

9 = I (3 + 9) ⇒ I = 1A

⇒ potential difference across 3 ω resistance = 3V and potential difference across 6 Ω resistance= 6V

⇒ p.d. across 3 μF capacitor = 3V and p.d. across 6μF capacitor =6V

∴ Charge on 3 μF capacitor,Q₁= 3 × 3 = 9μC

Charge on 6μF capacitor, Q₂ = 6× 6 = 36 μC

⇒ Charge (–Q₁) is shifted from the positive plate of 6μF capacitor. The remaining charge on the positive plate of 6 μF capacitor is shifted through the switch.

∴ Charge passing through the switch

= 36 – 9 = 27 μC

In the electric field of an point charge q, a certain charge is carried from point A to B, C, D and E. Then the work done is

least along the path AB
least along the path AD
zero alongany one of the path AB, AC, AD and AE
least along AE

Solution

Since, all A, B, C, D and E lie on an equipotential surface so,

A solid conducting sphere having a charge Q is surrounding by an uncharged concentric conducting hollow spherical shell. Let the potential difference between the surface of the solid sphere and that of the outer surface of the hollow shell be V. If the shell is now given a charge of – 3Q, the new potential difference between the same two surfaces is

V
2 V
4 V
– 2 V

Solution

A parallel plate capacitor of capacitance C is connected to a battery and is charged to a potential difference V. Another capacitor of capacitance 2C is similary charged to a potential difference 2V. The charging battery is now disconnected and the capacitors are connected in parallel to each other in such a way that the positive terminal of one is connected to the negative terminal of the other. The final energy of the configuration is

zero
³⁄₂CV²
²⁵⁄₆CV²
⁹⁄₂CV²

Solution

In a hollow spherical shell, potential (V)changes with respect to distance (s) from centre as

Solution

UnAttempted

0

Attempted

0

Correct

0

Wrong

0

Complete